Μπορεί άραγε κάτι που έχει να κάνει με τα Μαθηματικά να έχει ταυτόχρονα γλύκα; Μπορούμε να κάνουμε Μαθηματικά και να χαιρόμαστε συγχρόνως; Μπορεί το παίδεμα για να λύσουμε ένα δύσκολο πρόβλημα να είναι συναρπαστικό; Η προσπάθεια που γίνεται εδώ, φιλοδοξεί να αποδείξει ότι οι απαντήσεις στα παραπάνω ερωτήματα μπορούν να είναι ΝΑΙ! Μπορείτε να στέλνετε τις λύσεις σας, τις ερωτήσεις, τις παρατηρήσεις σας και δικά σας προβλήματα στη διεύθυνση mathsweets@gmail.com
Μαθηματικοί Διαγωνισμοί
Πέμπτη 4 Δεκεμβρίου 2014
Δευτέρα 24 Νοεμβρίου 2014
Τετάρτη 19 Νοεμβρίου 2014
Κυριακή 18 Μαΐου 2014
Παραγοντοποίηση παράστασης
Να παραγοντοποιήσετε την παράσταση:
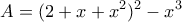
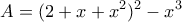
Ετικέτες
Γ΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Πώς με τις ταυτότητες λύνουμε ένα ενδιαφέρον πρόβλημα
α) Να κάνετε τις πράξεις:
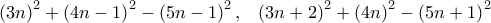
(β) Χρησιμοποιώντας το (α) ή και με άλλο τρόπο να γράψετε τους αριθμούς και
και  στη μορφή
στη μορφή 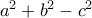 όπου οι
όπου οι  είναι ακέραιοι με
είναι ακέραιοι με 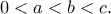
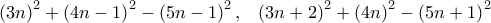
(β) Χρησιμοποιώντας το (α) ή και με άλλο τρόπο να γράψετε τους αριθμούς
 και
και  στη μορφή
στη μορφή 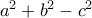 όπου οι
όπου οι  είναι ακέραιοι με
είναι ακέραιοι με 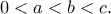
Διαδοχικά τετράγωνα φυσικών
Oι  είναι τρεις θετικοί ακέραιοι ώστε οι
είναι τρεις θετικοί ακέραιοι ώστε οι 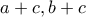 να είναι τα τετράγωνα δύο διαδοχικών φυσικών αριθμών.
να είναι τα τετράγωνα δύο διαδοχικών φυσικών αριθμών.
 είναι τρεις θετικοί ακέραιοι ώστε οι
είναι τρεις θετικοί ακέραιοι ώστε οι 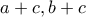 να είναι τα τετράγωνα δύο διαδοχικών φυσικών αριθμών.
να είναι τα τετράγωνα δύο διαδοχικών φυσικών αριθμών.
Να αποδείξετε ότι οι  είναι επίσης τετράγωνα δύο διαδοχικών φυσικών αριθμών.
είναι επίσης τετράγωνα δύο διαδοχικών φυσικών αριθμών.
 είναι επίσης τετράγωνα δύο διαδοχικών φυσικών αριθμών.
είναι επίσης τετράγωνα δύο διαδοχικών φυσικών αριθμών.
Ετικέτες
Γ΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Εγγραφή σε:
Σχόλια (Atom)



