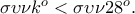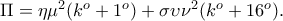Στο ορθογώνιο 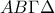 του παραπάνω σχήματος
του παραπάνω σχήματος
Α. να αποδείξετε ότι:
α)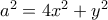
β)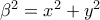
γ)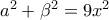
δ)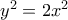
ε)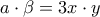
Β. να υπολογίσετε τους λόγους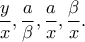
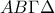 του παραπάνω σχήματος
του παραπάνω σχήματος Α. να αποδείξετε ότι:
α)
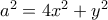
β)
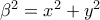
γ)
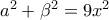
δ)
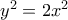
ε)
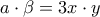
Β. να υπολογίσετε τους λόγους
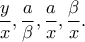
Μπορεί άραγε κάτι που έχει να κάνει με τα Μαθηματικά να έχει ταυτόχρονα γλύκα; Μπορούμε να κάνουμε Μαθηματικά και να χαιρόμαστε συγχρόνως; Μπορεί το παίδεμα για να λύσουμε ένα δύσκολο πρόβλημα να είναι συναρπαστικό; Η προσπάθεια που γίνεται εδώ, φιλοδοξεί να αποδείξει ότι οι απαντήσεις στα παραπάνω ερωτήματα μπορούν να είναι ΝΑΙ! Μπορείτε να στέλνετε τις λύσεις σας, τις ερωτήσεις, τις παρατηρήσεις σας και δικά σας προβλήματα στη διεύθυνση mathsweets@gmail.com
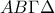 του παραπάνω σχήματος
του παραπάνω σχήματος 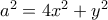
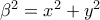
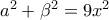
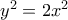
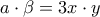
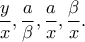
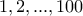 σε μια ευθεία γραμμή με όποια σειρά θέλουμε. Υπάρχει τρόπος να τους
βάλουμε έτσι ώστε η απόλυτη τιμή της διαφοράς δύο οποιωνδήποτε
διαδοχικών αριθμών να είναι τουλάχιστον
σε μια ευθεία γραμμή με όποια σειρά θέλουμε. Υπάρχει τρόπος να τους
βάλουμε έτσι ώστε η απόλυτη τιμή της διαφοράς δύο οποιωνδήποτε
διαδοχικών αριθμών να είναι τουλάχιστον 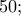

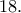 Βρείτε το ψηφίο
Βρείτε το ψηφίο 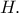
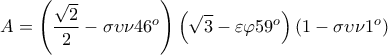 είναι θετικός, αρνητικός ή μηδέν;
είναι θετικός, αρνητικός ή μηδέν; και εφΓ=
και εφΓ=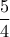 .
.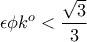 και
και