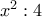Να λύσετε την εξίσωση
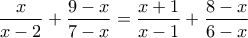
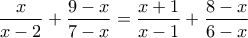
Μπορεί άραγε κάτι που έχει να κάνει με τα Μαθηματικά να έχει ταυτόχρονα γλύκα; Μπορούμε να κάνουμε Μαθηματικά και να χαιρόμαστε συγχρόνως; Μπορεί το παίδεμα για να λύσουμε ένα δύσκολο πρόβλημα να είναι συναρπαστικό; Η προσπάθεια που γίνεται εδώ, φιλοδοξεί να αποδείξει ότι οι απαντήσεις στα παραπάνω ερωτήματα μπορούν να είναι ΝΑΙ! Μπορείτε να στέλνετε τις λύσεις σας, τις ερωτήσεις, τις παρατηρήσεις σας και δικά σας προβλήματα στη διεύθυνση mathsweets@gmail.com


 έχει νόημα η παράσταση
έχει νόημα η παράσταση 

 αν επιπλέον γνωρίζετε ότι
αν επιπλέον γνωρίζετε ότι 
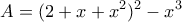
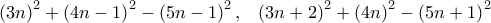
 και
και  στη μορφή
στη μορφή 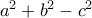 όπου οι
όπου οι  είναι ακέραιοι με
είναι ακέραιοι με 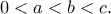
 είναι τρεις θετικοί ακέραιοι ώστε οι
είναι τρεις θετικοί ακέραιοι ώστε οι 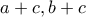 να είναι τα τετράγωνα δύο διαδοχικών φυσικών αριθμών.
να είναι τα τετράγωνα δύο διαδοχικών φυσικών αριθμών.  είναι επίσης τετράγωνα δύο διαδοχικών φυσικών αριθμών.
είναι επίσης τετράγωνα δύο διαδοχικών φυσικών αριθμών. είναι δυο θετικοί ακέραιοι τέτοιοι ώστε η ευκλείδεια διαίρεση
είναι δυο θετικοί ακέραιοι τέτοιοι ώστε η ευκλείδεια διαίρεση  να αφήνει υπόλοιπο
να αφήνει υπόλοιπο  ενώ η ευκλείδεια διαίρεση
ενώ η ευκλείδεια διαίρεση  να αφήνει υπόλοιπο
να αφήνει υπόλοιπο  . Να βρείτε το υπόλοιπο των παρακάτω ευκλείδειων διαιρέσεων:
. Να βρείτε το υπόλοιπο των παρακάτω ευκλείδειων διαιρέσεων: