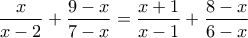Μπορεί άραγε κάτι που έχει να κάνει με τα Μαθηματικά να έχει ταυτόχρονα γλύκα; Μπορούμε να κάνουμε Μαθηματικά και να χαιρόμαστε συγχρόνως; Μπορεί το παίδεμα για να λύσουμε ένα δύσκολο πρόβλημα να είναι συναρπαστικό; Η προσπάθεια που γίνεται εδώ, φιλοδοξεί να αποδείξει ότι οι απαντήσεις στα παραπάνω ερωτήματα μπορούν να είναι ΝΑΙ! Μπορείτε να στέλνετε τις λύσεις σας, τις ερωτήσεις, τις παρατηρήσεις σας και δικά σας προβλήματα στη διεύθυνση mathsweets@gmail.com
Μαθηματικοί Διαγωνισμοί
Τρίτη 25 Απριλίου 2017
Σάββατο 22 Απριλίου 2017
Χριστός Ανέστη!
Γιαννης, Ριτσος, «Εαρινη Συμφωνια» (αποσπασμα)
Άκου τα σήμαντρα των εξοχικών εκκλησιών. Φτάνουν από πολύ μακριά από πολύ βαθιά. Απ’ τα χείλη των παιδιών απ’ την άγνοια των χελιδονιών απ’ τις άσπρες αυλές της Κυριακής απ’ τ’ αγιοκλήματα και τους περιστεριώνες των ταπεινών σπιτιών.Χριστός Ανέστη!
Κυριακή 9 Απριλίου 2017
Κυριακή των Βαΐων II
Το ABCD είναι τετράγωνο και το P είναι σημείο της πλευράς CD με PC=4PD.
Η μεσοκάθετος του PC τέμνει την BD στο S. Αν το τρίγωνο APS έχει εμβαδόν 650 τ.εκ. να βρείτε το μήκος της πλευράς του τετραγώνου.
Η μεσοκάθετος του PC τέμνει την BD στο S. Αν το τρίγωνο APS έχει εμβαδόν 650 τ.εκ. να βρείτε το μήκος της πλευράς του τετραγώνου.
Παρασκευή 31 Μαρτίου 2017
Eπαναληπτική άσκηση για το Γ1 και το Γ4!
Δίνονται οι παραστάσεις


(α) Να αποδείξετε ότι
(β) Να αποδείξετε ότι
(γ) Να βρείτε τους αριθμούς αν επιπλέον γνωρίζετε ότι
αν επιπλέον γνωρίζετε ότι 


(α) Να αποδείξετε ότι

(β) Να αποδείξετε ότι

(γ) Να βρείτε τους αριθμούς
 αν επιπλέον γνωρίζετε ότι
αν επιπλέον γνωρίζετε ότι 
Δευτέρα 27 Μαρτίου 2017
Τετάρτη 28 Δεκεμβρίου 2016
Κυριακή 4 Δεκεμβρίου 2016
Τετάρτη 16 Νοεμβρίου 2016
Δευτέρα 4 Ιουλίου 2016
Τετάρτη 18 Μαΐου 2016
Τρίτη 17 Μαΐου 2016
Παρασκευή 4 Δεκεμβρίου 2015
Δευτέρα 16 Νοεμβρίου 2015
Δευτέρα 18 Μαΐου 2015
Η αλλαγή κοστίζει μόνο ένα λεπτό!
Μια παρέα παιδιών μπαίνει σε ένα βιβλιοπωλείο.
Αν κάθε αγόρι αγοράσει από ένα μολύβι και κάθε κορίτσι αγοράσει από ένα στυλό τότε θα πληρώσουν όλοι μαζί ένα λεπτό περισσότερο απ΄ ότι θα πλήρωναν αν κάθε αγόρι αγόραζε από ένα στυλό και κάθε κορίτσι αγόραζε από ένα μολύβι. Γνωρίζουμε ότι τα αγόρια είναι περισσότερα από τα κορίτσια. Ποια είναι η διαφορά του πλήθους των κοριτσιών από το πλήθος των αγοριών;
Αν κάθε αγόρι αγοράσει από ένα μολύβι και κάθε κορίτσι αγοράσει από ένα στυλό τότε θα πληρώσουν όλοι μαζί ένα λεπτό περισσότερο απ΄ ότι θα πλήρωναν αν κάθε αγόρι αγόραζε από ένα στυλό και κάθε κορίτσι αγόραζε από ένα μολύβι. Γνωρίζουμε ότι τα αγόρια είναι περισσότερα από τα κορίτσια. Ποια είναι η διαφορά του πλήθους των κοριτσιών από το πλήθος των αγοριών;
Ετικέτες
Γ΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Παραγοντοποίηση από την Ινδία
Να παραγοντοποιήσετε την παράσταση

Ετικέτες
Γ΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Κυριακή 17 Μαΐου 2015
Κλασματική εξίσωση (2)
Δίνεται η παράσταση

α) Για ποιες τιμές του έχει νόημα η παράσταση
έχει νόημα η παράσταση 
β) Να απλοποιήσετε την παράσταση

α) Για ποιες τιμές του
 έχει νόημα η παράσταση
έχει νόημα η παράσταση 
β) Να απλοποιήσετε την παράσταση

γ) Να βρείτε τον  αν επιπλέον γνωρίζετε ότι
αν επιπλέον γνωρίζετε ότι 
 αν επιπλέον γνωρίζετε ότι
αν επιπλέον γνωρίζετε ότι 
Παρασκευή 24 Απριλίου 2015
Εγγραφή σε:
Αναρτήσεις (Atom)






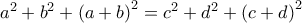 , να αποδείξετε ότι
, να αποδείξετε ότι