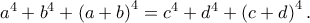1) Να σχεδιάσετε με ένα μοιρογνωμόνιο τρεις διαδοχικές γωνίες

 και
και 
Κατασκευάστε τη διχοτόμο ΟΖ της γωνίας
 Κατόπιν υπολογίστε χωρίς μοιρογνωμόνιο τις γωνίες
Κατόπιν υπολογίστε χωρίς μοιρογνωμόνιο τις γωνίες (i)

(ii)

2) Να βρείτε δύο συμπληρωματικές γωνίες που διαφέρουν κατά 30 μοίρες.
3) Να βρείτε δύο παραπληρωματικές γωνίες που διαφέρουν κατά 10 μοίρες.
4) Να βρείτε δύο συμπληρωματικές γωνίες ώστε η μία να είναι τετραπλάσια της άλλης.
5) Να βρείτε δύο παραπληρωματικές γωνίες ώστε η μία να είναι οκταπλάσια της άλλης.





















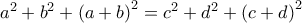 , να αποδείξετε ότι
, να αποδείξετε ότι