Μπορεί άραγε κάτι που έχει να κάνει με τα Μαθηματικά να έχει ταυτόχρονα γλύκα; Μπορούμε να κάνουμε Μαθηματικά και να χαιρόμαστε συγχρόνως; Μπορεί το παίδεμα για να λύσουμε ένα δύσκολο πρόβλημα να είναι συναρπαστικό; Η προσπάθεια που γίνεται εδώ, φιλοδοξεί να αποδείξει ότι οι απαντήσεις στα παραπάνω ερωτήματα μπορούν να είναι ΝΑΙ! Μπορείτε να στέλνετε τις λύσεις σας, τις ερωτήσεις, τις παρατηρήσεις σας και δικά σας προβλήματα στη διεύθυνση mathsweets@gmail.com
Μαθηματικοί Διαγωνισμοί
Δευτέρα 16 Νοεμβρίου 2015
Δευτέρα 18 Μαΐου 2015
Η αλλαγή κοστίζει μόνο ένα λεπτό!
Μια παρέα παιδιών μπαίνει σε ένα βιβλιοπωλείο.
Αν κάθε αγόρι αγοράσει από ένα μολύβι και κάθε κορίτσι αγοράσει από ένα στυλό τότε θα πληρώσουν όλοι μαζί ένα λεπτό περισσότερο απ΄ ότι θα πλήρωναν αν κάθε αγόρι αγόραζε από ένα στυλό και κάθε κορίτσι αγόραζε από ένα μολύβι. Γνωρίζουμε ότι τα αγόρια είναι περισσότερα από τα κορίτσια. Ποια είναι η διαφορά του πλήθους των κοριτσιών από το πλήθος των αγοριών;
Αν κάθε αγόρι αγοράσει από ένα μολύβι και κάθε κορίτσι αγοράσει από ένα στυλό τότε θα πληρώσουν όλοι μαζί ένα λεπτό περισσότερο απ΄ ότι θα πλήρωναν αν κάθε αγόρι αγόραζε από ένα στυλό και κάθε κορίτσι αγόραζε από ένα μολύβι. Γνωρίζουμε ότι τα αγόρια είναι περισσότερα από τα κορίτσια. Ποια είναι η διαφορά του πλήθους των κοριτσιών από το πλήθος των αγοριών;
Ετικέτες
Γ΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Παραγοντοποίηση από την Ινδία
Να παραγοντοποιήσετε την παράσταση

Ετικέτες
Γ΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Κυριακή 17 Μαΐου 2015
Κλασματική εξίσωση (2)
Δίνεται η παράσταση

α) Για ποιες τιμές του έχει νόημα η παράσταση
έχει νόημα η παράσταση 
β) Να απλοποιήσετε την παράσταση

α) Για ποιες τιμές του
 έχει νόημα η παράσταση
έχει νόημα η παράσταση 
β) Να απλοποιήσετε την παράσταση

γ) Να βρείτε τον  αν επιπλέον γνωρίζετε ότι
αν επιπλέον γνωρίζετε ότι 
 αν επιπλέον γνωρίζετε ότι
αν επιπλέον γνωρίζετε ότι 
Παρασκευή 24 Απριλίου 2015
Πέμπτη 4 Δεκεμβρίου 2014
Δευτέρα 24 Νοεμβρίου 2014
Τετάρτη 19 Νοεμβρίου 2014
Κυριακή 18 Μαΐου 2014
Παραγοντοποίηση παράστασης
Να παραγοντοποιήσετε την παράσταση:
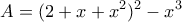
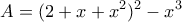
Ετικέτες
Γ΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Πώς με τις ταυτότητες λύνουμε ένα ενδιαφέρον πρόβλημα
α) Να κάνετε τις πράξεις:
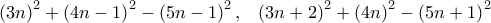
(β) Χρησιμοποιώντας το (α) ή και με άλλο τρόπο να γράψετε τους αριθμούς και
και  στη μορφή
στη μορφή 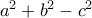 όπου οι
όπου οι  είναι ακέραιοι με
είναι ακέραιοι με 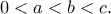
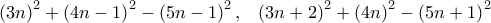
(β) Χρησιμοποιώντας το (α) ή και με άλλο τρόπο να γράψετε τους αριθμούς
 και
και  στη μορφή
στη μορφή 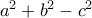 όπου οι
όπου οι  είναι ακέραιοι με
είναι ακέραιοι με 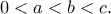
Διαδοχικά τετράγωνα φυσικών
Oι  είναι τρεις θετικοί ακέραιοι ώστε οι
είναι τρεις θετικοί ακέραιοι ώστε οι 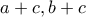 να είναι τα τετράγωνα δύο διαδοχικών φυσικών αριθμών.
να είναι τα τετράγωνα δύο διαδοχικών φυσικών αριθμών.
 είναι τρεις θετικοί ακέραιοι ώστε οι
είναι τρεις θετικοί ακέραιοι ώστε οι 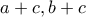 να είναι τα τετράγωνα δύο διαδοχικών φυσικών αριθμών.
να είναι τα τετράγωνα δύο διαδοχικών φυσικών αριθμών.
Να αποδείξετε ότι οι  είναι επίσης τετράγωνα δύο διαδοχικών φυσικών αριθμών.
είναι επίσης τετράγωνα δύο διαδοχικών φυσικών αριθμών.
 είναι επίσης τετράγωνα δύο διαδοχικών φυσικών αριθμών.
είναι επίσης τετράγωνα δύο διαδοχικών φυσικών αριθμών.
Ετικέτες
Γ΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Σάββατο 16 Νοεμβρίου 2013
Σάββατο 18 Μαΐου 2013
Μερικές ευκλείδειες διαιρέσεις
Οι αριθμοί  είναι δυο θετικοί ακέραιοι τέτοιοι ώστε η ευκλείδεια διαίρεση
είναι δυο θετικοί ακέραιοι τέτοιοι ώστε η ευκλείδεια διαίρεση  να αφήνει υπόλοιπο
να αφήνει υπόλοιπο  ενώ η ευκλείδεια διαίρεση
ενώ η ευκλείδεια διαίρεση  να αφήνει υπόλοιπο
να αφήνει υπόλοιπο  . Να βρείτε το υπόλοιπο των παρακάτω ευκλείδειων διαιρέσεων:
. Να βρείτε το υπόλοιπο των παρακάτω ευκλείδειων διαιρέσεων:
(α)
(β)
(γ)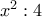
(δ)
 είναι δυο θετικοί ακέραιοι τέτοιοι ώστε η ευκλείδεια διαίρεση
είναι δυο θετικοί ακέραιοι τέτοιοι ώστε η ευκλείδεια διαίρεση  να αφήνει υπόλοιπο
να αφήνει υπόλοιπο  ενώ η ευκλείδεια διαίρεση
ενώ η ευκλείδεια διαίρεση  να αφήνει υπόλοιπο
να αφήνει υπόλοιπο  . Να βρείτε το υπόλοιπο των παρακάτω ευκλείδειων διαιρέσεων:
. Να βρείτε το υπόλοιπο των παρακάτω ευκλείδειων διαιρέσεων:(α)

(β)

(γ)
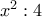
(δ)

Ετικέτες
Γ΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Προπόνηση στην ταυτότητα $(α+β+γ)^2$
Για τους αριθμούς $a, b, c$ ισχύουν οι σχέσεις $a+b+c=0$ και $a^2+b^2+c^2=1.$
Να βρείτε την αριθμητική τιμή της παράστασης $a^4+b^4+c^4.$
Να βρείτε την αριθμητική τιμή της παράστασης $a^4+b^4+c^4.$
Ετικέτες
Γ΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Παρασκευή 17 Μαΐου 2013
Μαθηματικές Λιχουδιές, Τεύχος 6ο
Λίγο πριν το τέλος της σχολικής χρονιάς κυκλοφόρησε το 6ο τεύχος της εφημερίδας μας Μαθηματικές Λιχουδιές. Το μεράκι και η προσπάθεια των παιδιών που συμμετείχαν είχαν ως αποτέλεσμα αυτό το τεύχος να ξεπεράσει κάθε προσδοκία μας.
Ιδιαίτερη χαρά μας έδωσαν δύο συνεντεύξεις: η πρώτη με την ηθοποιό, σκηνοθέτη και συγγραφέα κ. Κάρμεν Ρουγγέρη και η δεύτερη με τον χρυσό Ολυμπιονίκη της Διεθνούς μαθηματικής ολυμπιάδας 2012, Παναγιώτη Λώλα.
Τους ευχαριστούμε και τους δύο θερμά!
Πολλά συγχαρητήρια σε όλα τα παιδιά της συντακτικής ομάδας και θερμές ευχαριστίες στους συναδέλφους που στήριξαν αυτήν την προσπάθεια.
Καλό καλοκαίρι!
Δευτέρα 24 Δεκεμβρίου 2012
Παρασκευή 14 Δεκεμβρίου 2012
Εγγραφή σε:
Αναρτήσεις (Atom)