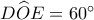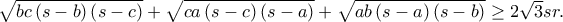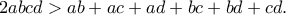Τέσσερις γραφικές παραστάσεις για τα παιδιά του Β1!

Για την Παρασκευή 18/12/2020

(α) Nα βρείτε τη μέγιστη τιμή, την ελάχιστη τιμή και την περίοδο,

(β) να σχεδιάσετε τη γραφική παράσταση σε διάστημα πλάτους μιας περιόδου

των συναρτήσεων

1. f(x) = 2ημ4x - 3

2. g(x) = 3συν6x - 5

3. h(x) = -3ημ2x+4

4. k(x) = -4συν3x + 3  

Με τη βοήθεια των γραφικών παραστάσεων που θα έχετε κάνει, γράψτε τα διαστήματα μονοτονίας των συναρτήσεων και τις θέσεις των ακροτάτων τους.

Εργασία Γεωμετρίας για τα παιδιά του Α4!

 Έως και την ερχόμενη Τρίτη 15/12/2020 να λύσετε τις παρακάτω ασκήσεις και να μου τις στείλετε στη 

διεύθυνση mathsweets@gmail.com

Εργασία Γεωμετρίας για τα παιδιά του Α4

Ορισμός συνέχειας, θεώρημα Bolzano και συνέπειες

 Συνέχεια συνάρτησης και θεώρημα Bolzano

Θεώρημα Bolzano και συνέπειες

Πυθαγόρειο θεώρημα

Πυθαγόρειο θεώρημα  (συλλογή με 43 ασκήσεις)

Δύο διαγωνίσματα στα διανύσματα

 1ο διαγώνισμα στα διανύσματα

2ο διαγώνισμα στα διανύσματα

Επαναληπτικές ασκήσεις στα διανύσματα (Μέρος 1ο)

 Επαναληπτικές ασκήσεις στο κεφάλαιο των διανυσμάτων (Μέρος 1ο)

Για το Βθετ1:

 Λύστε τις ασκήσεις 

                   2, 3, 5(α)(β), 8, 9, 10, 11, 12. 

Στείλτε τις λύσεις σας έως τη Δευτέρα 7/12/2020 στη διεύθυνση

mathsweets@gmail.com

Όριο συνάρτησης στο άπειρο

 Όριο συνάρτησης στο άπειρο

Μη πεπερασμένο όριο στο χο

 Για προπόνηση στα μη πεπερασμένα όρια στο χο

Ασκήσεις τριγωνομετρίας για το Β1!

 ① Σε έναν τριγωνομετρικό κύκλο να τοποθετήσετε τη γωνία 220⁰ και να προσδιορίσετε τη            θέση των αριθμών: ημ220⁰ , συν220⁰ , εφ220⁰

② Σε έναν τριγωνομετρικό κύκλο να τοποθετήσετε μια γωνία ω ώστε εφω = -2 αν γνωρίζετε       ότι η τελική της πλευρά περιέχεται στο 4ο τεταρτημόριο.

③  Να βρείτε το πρόσημο του αριθμού Α = ημ200⁰·συν300⁰·εφ4000⁰·σφ1000⁰

④  Να υπολογίσετε την αριθμητική τιμή της παράστασης 

                                 Α = εφ780⁰·σφ1140⁰·συν4500⁰·ημ1530⁰

⑤ Να υπολογίσετε τους τριγωνομετρικούς αριθμούς των γωνιών 

     α) 17π   β) -13π  

Ασκήσεις γεωμετρίας από την παλιά τράπεζα θεμάτων (Μέρος 1ο)

 Πρόκειται για μια ενδιαφέρουσα συλλογή ασκήσεων. Είναι ταξινομημένες σε κεφάλαια.

Επίσης είναι χωρισμένες σε δύο κατηγορίες, 2ο θέμα (συνήθως ευκολότερες) και 4ο θέμα (συνήθως δυσκολότερες)

Δείτε εδώ το 1ο μέρος.

Δραστηριότητες στην τριγωνική ανισότητα

 

Τέσσερις ασκήσεις στον συντελεστή διεύθυνσης του Γιώργου Μαυρίδη

 

Ασκήσεις στο εσωτερικό γινόμενο

 Ασκήσεις στο εσωτερικό γινόμενο (Μέρος Α΄)

Υλικό για το 2ο κεφάλαιο της Άλγεβρας Β΄ Λυκείου

❶ Ασκήσεις στην κατακόρυφη-οριζόντια μετατόπιση καμπύλης

❷ Θέματα από την παλιά τράπεζα θεμάτων για το 2ο κεφάλαιο

❸ Συνδυαστικά θέματα του 2ου κεφαλαίου

Η επιμέλεια των παραπάνω ανήκει στον συνάδελφο Παύλο Παλαιολόγου και τον ευχαριστούμε πολύ.  

Μία συλλογή ασκήσεων στα πεπερασμένα όρια στο χ_ο

 Όριο στο χ_ο (Μέρος 1ο)

Όριο στο χ_ο (Μέρος 2ο) 

Τριγωνομετρικά Όρια - Όρια Σύνθετης Συνάρτησης

Τριγωνομετρικά Όρια-Όρια Σύνθετης Συνάρτησης

Η έννοια του ορίου

 Μια παρουσίαση της έννοιας του ορίου εδώ.

Διαγωνίσματα μέχρι την αντίστροφη συνάρτηση

 1) Ένα διαγώνισμα του Ιωάννη Σαράφη εδώ.

2) Ένα διαγώνισμα του Χρήστου Πατήλα εδώ.

 

Ασκήσεις στις συναρτήσεις (Ι)

 Μια συλλογή ασκήσεων για τις παραγράφους 1.1 έως 1.3 μπορείτε να βρείτε εδώ.

Τέσσερις αριθμοί στο διάστημα [0,1]

Διαγωνισμός Πόλεων, 1995

                  

     

Κλάσμα με τεράστιους όρους

Να αποδείξετε ότι $\dfrac{0,12345678...4748495051}{0,5150494847...87654321}=0,239...$  (Μόσχα, 1951)

Εξίσωση

Να λυθεί η εξίσωση

Σωτήρης Λουρίδας, Αθήνα

Δύο πενταψήφιοι με πηλίκο 9

Να προσδιοριστούν όλα τα ζεύγη πενταψήφιων  φυσικών αριθμών m, n για τους οποίους γνωρίζουμε ότι για να τους γράψουμε θα χρησιμοποιήσουμε όλα τα ψηφία 0, 1, 2,..., 9 και επιπλέον m=9n.

Σωτήρης Λουρίδας, Αθήνα

Διπλή ανισότητα

Μάγκος Θάνος, Θεσσαλονίκη

Δεν είναι δυνατόν και οι τρεις να είναι τέλεια τετράγωνα

Έστω $a, b, c$ τρεις θετικοί ακέραιοι. Να δείξετε ότι δεν είναι δυνατόν οι αριθμοί 

$$a^2+b+c, b^2+a+c, c^2+a+b$$

να είναι και οι τρεις τέλεια τετράγωνα.

20 ακέραιοι με άθροισμα θετικό, κάθε τρεις διαδοχικοί με άθροισμα αρνητικό

α) Να δείξετε ότι μπορούμε να τοποθετήσουμε 20 μη μηδενικούς ακεραίους, όχι απαραίτητα διαφορετικούς, στη σειρά έτσι ώστε το άθροισμά τους να είναι θετικό, ενώ το άθροισμα οποιωνδήποτε τριών διαδοχικών να είναι αρνητικό.
β) Δείξτε ότι δε μπορούμε να κάνουμε το ίδιο σε ένα κύκλο.

Ένας τουλάχιστον είναι ίσος με 1

Για τους πραγματικούς αριθμούς a, b, c ισχύουν: 

abc=1 και ab+bc+ca=a+b+c. 

Να αποδείξετε ότι ένας τουλάχιστον από τους αριθμούς αυτούς είναι ίσος με το 1.

Ανισότητα με πλευρές τριγώνου και τρεις τυχαίους πραγματικούς

Αν  πλευρές τριγώνου και  πραγματικοί, να δείξετε ότι :

.

Πότε ισχύει η ισότητα;

Παναγιώτης Λώλας

Ελάχιστο παράστασης

Να υπολογιστεί το ελάχιστο της παράστασης

$$x^2-8xy+19y^2-6y+3$$
προσδιορίζοντας ταυτόχρονα και τις τιμές των $x,y$ για τις οποίες το έχουμε.

Ανισότητα ακεραίων

Αν  είναι θετικοί ακέραιοι να αποδείξετε ότι 

                                

                  Θεαίτητος, 1ο τεύχος

Μανόλης Μαραγκάκης

Προπολεμικό πρόβλημα! (1938-39)

Σε ορθογώνιο τρίγωνο  (με ορθή γωνία ) δίνονται οι τρεις πλευρές .
Να βρεθεί πάνω στην υποτείνουσα  σημείο  τέτοιο ώστε ο λόγος  να είναι ίσος με . (Διερεύνηση)

Πανελλήνιος Μαθηματικός Διαγωνισμός, 1938-39

(Πρακτικού Λυκείου)

Ανίσωση με ριζικό

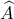
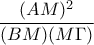
Να λυθεί στο  η ανίσωση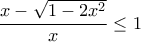

Να βρεθεί η συνάρτηση

Σύνολα ακεραίων

Προσδιορίστε όλα τα σύνολα  θετικών ακεραίων τέτοια ώστε για οποιαδήποτε δύο,

όχι απαραίτητα διαφορετικά, στοιχεία  του  ο αριθμός  να ανήκει στο 

Ανισότητα με ολοκλήρωμα

Λάμπρος Μπαλός, Τρίκαλα

Το άθροισμά τους είναι ίσο με το ΕΚΠ τους!

α) Να βρείτε τρεις θετικούς ακέραιους αριθμούς με την ιδιότητα το άθροισμά τους να είναι ίσο με το ελάχιστο κοινό πολλαπλάσιό τους.

β) Να βρείτε 100 θετικούς ακέραιους αριθμούς με την ιδιότητα το άθροισμά τους να είναι ίσο με το ελάχιστο κοινό πολλαπλάσιό τους.
                                                               Διαγωνισμός Πόλεων, 1995

γ) Να βρείτε 2020 θετικούς ακέραιους αριθμούς με την ιδιότητα το άθροισμά τους να είναι ίσο με το ελάχιστο κοινό πολλαπλάσιό τους.

                       

Γωνία 60 μοιρών με κορυφή το περίκεντρο ισοπλεύρου τριγώνου

Δίνεται ισόπλευρο τρίγωνο  με πλευρά  και περίκεντρο . Επί των πλευρών  παίρνουμε αντίστοιχα σημεία , τέτοια ώστε . Δείξτε ότι η περίμετρος του τριγώνου  ισούται με .

 Μιχάλης Νάννος, Σαλαμίνα

Κάπου υπάρχει λάθος

Σ' ένα χορό πήραν μέρος 8 αγόρια και 8 κορίτσια. Κάθε αγόρι χόρεψε με μερικά κορίτσια και κάθε κορίτσι με μερικά αγόρια. Μετά το τέλος του χορού κάθε άτομο έγραψε, στη σειρά, τον αριθμό των χορών που χόρεψε. Έτσι πήραμε τους αριθμούς: 3, 3, 3, 3, 3, 3, 4, 6, 6, 6, 6, 6, 6, 6, 6, 6. Να αποδείξετε ότι οι αριθμοί αυτοί δεν είναι οι σωστοί, γιατί κάπου υπάρχει λάθος.

Ευκλείδης, Β' Γυμνασίου, 1995

Ανισότητα με πλευρές τριγώνου (1)

Σε τρίγωνο  αποδείξτε ότι

Διευκρίνηση: a, b, c είναι οι πλευρές του τριγώνου

                    s είναι η ημιπερίμετρος του τριγώνου

                    r είναι η ακτίνα του εγγεγραμμένου κύκλου του τριγώνου

             

Ανισότητα με 4 ακεραίους

Αν  είναι τέσσερις διαφορετικοί θετικοί ακέραιοι, να αποδείξετε ότι

Ιδιότητα της διαμέσου

Καραντάνας Θανάσης

Γεωμετρικός τόπος βαρύκεντρου

Γιώργος Βισβίκης, Αθήνα

Κύκλοι, τρίγωνα, τετράπλευρα, εμβαδά

Υπολογισμός αθροίσματος κλασμάτων

Συγκρίσεις

Θαλής, Β' Γυμνασίου, 1995

200 αυγά

Έχουμε 200 αυγά τα οποία θέλουμε να τοποθετήσουμε σε καλάθια κατά τέτοιο τρόπο, ώστε κάθε καλάθι να περιέχει διαφορετικό αριθμό αυγών. Ποιος είναι ο μέγιστος αριθμός καλαθιών που μπορούν να χρησιμοποιηθούν σε αυτή τη διαδικασία;

Θαλής, Β' Γυμνασίου, 1995

Στρατηγική σε πολύγωνο με άρτιο πλήθος πλευρών

Δυο μαθητές Α και Β παίζουν το ακόλουθο παιχνίδι:
Τους δίνεται ένα κανονικό πολύγωνο με άρτιο πλήθος πλευρών, μεγαλύτερο από 6 (π.χ.ένα 100-γωνο). Κάθε παίκτης συνδέει δυο από τις κορυφές του πολυγώνου με ένα τμήμα το οποίο, όμως, να μην τέμνει κανένα από άλλα τέτοια τμήματα που οι παίκτες είχαν φέρει προηγουμένως. Θα χάσει ο παίκτης που πρώτος δε θα μπορέσει να φέρει ένα τέτοιο τμήμα. Μπορεί ένας παίκτης να ακολουθήσει μια στρατηγική ώστε να νικήσει σίγουρα;

Θαλής, Α' Λυκείου, 1995

Ο ταμίας έχει περισσότερα νομίσματα των 20 λεπτών από αυτά των 10 λεπτών.

Ένας ταμίας έχει 500 λεπτά σε νομίσματα των 10, 15, 20 λεπτών. Ο συνολικός αριθμός των νομισμάτων είναι 30. Να αποδείξετε ότι ο ταμίας έχει περισσότερα νομίσματα των 20 λεπτών από αυτά των 10 λεπτών.

Διαγωνισμός πόλεων, 1995

Οι τρεις ακρίδες

Τρεις ακρίδες Α, Β, Γ βρίσκονται πάνω σε μία ευθεία. Η  Β βρίσκεται στο μέσο μεταξύ των Α και Γ. Κάθε δευτερόλεπτο μία απ' αυτές πηδά πάνω από μία από τις άλλες στο συμμετρικό σημείο ως προς τη δεύτερη. Μετά από μερικά άλματα οι ακρίδες έχουν επιστρέψει στα αρχικά σημεία, όχι κατ' ανάγκη η καθεμία στην αρχική της θέση. Να αποδείξετε ότι η Β επιστρέφει αναγκαστικά στην αρχική της θέση.

Διαγωνισμός Πόλεων, 1995

Ο πιο μικρός αριθμός που τελειώνει σε 38, διαιρείται με το 38, έχει άθροισμα ψηφίων το 38!

Βρείτε το μικρότερο φυσικό αριθμό ο οποίος τελειώνει σε 38, διαιρείται με το 38 και το άθροισμα των ψηφίων του είναι 38.

Μέγιστη και ελάχιστη τιμή

Ταυτότητα

8 ίσοι κύκλοι μέσα σε ορθογώνιο