Μπορεί άραγε κάτι που έχει να κάνει με τα Μαθηματικά να έχει ταυτόχρονα γλύκα; Μπορούμε να κάνουμε Μαθηματικά και να χαιρόμαστε συγχρόνως; Μπορεί το παίδεμα για να λύσουμε ένα δύσκολο πρόβλημα να είναι συναρπαστικό; Η προσπάθεια που γίνεται εδώ, φιλοδοξεί να αποδείξει ότι οι απαντήσεις στα παραπάνω ερωτήματα μπορούν να είναι ΝΑΙ! Μπορείτε να στέλνετε τις λύσεις σας, τις ερωτήσεις, τις παρατηρήσεις σας και δικά σας προβλήματα στη διεύθυνση mathsweets@gmail.com
Μαθηματικοί Διαγωνισμοί
Σάββατο 25 Ιουλίου 2020
Παρασκευή 24 Ιουλίου 2020
Κλάσμα με τεράστιους όρους
Να αποδείξετε ότι $\dfrac{0,12345678...4748495051}{0,5150494847...87654321}=0,239...$ (Μόσχα, 1951)
Δύο πενταψήφιοι με πηλίκο 9
Να προσδιοριστούν όλα τα ζεύγη πενταψήφιων φυσικών αριθμών m, n για τους οποίους γνωρίζουμε ότι για να τους γράψουμε θα χρησιμοποιήσουμε όλα τα ψηφία 0, 1, 2,..., 9 και επιπλέον m=9n.
Σωτήρης Λουρίδας, Αθήνα
Πέμπτη 23 Ιουλίου 2020
Δεν είναι δυνατόν και οι τρεις να είναι τέλεια τετράγωνα
Έστω $a, b, c$ τρεις θετικοί ακέραιοι. Να δείξετε ότι δεν είναι δυνατόν οι αριθμοί
$$a^2+b+c, b^2+a+c, c^2+a+b$$
να είναι και οι τρεις τέλεια τετράγωνα.
Ετικέτες
Μαθηματικοί Διαγωνισμοί
20 ακέραιοι με άθροισμα θετικό, κάθε τρεις διαδοχικοί με άθροισμα αρνητικό
α) Να δείξετε ότι μπορούμε να τοποθετήσουμε 20 μη μηδενικούς ακεραίους, όχι απαραίτητα διαφορετικούς, στη σειρά έτσι ώστε το άθροισμά τους να είναι θετικό, ενώ το άθροισμα οποιωνδήποτε τριών διαδοχικών να είναι αρνητικό.
β) Δείξτε ότι δε μπορούμε να κάνουμε το ίδιο σε ένα κύκλο.
β) Δείξτε ότι δε μπορούμε να κάνουμε το ίδιο σε ένα κύκλο.
Ετικέτες
Μαθηματικοί Διαγωνισμοί
Ένας τουλάχιστον είναι ίσος με 1
Για τους πραγματικούς αριθμούς a, b, c ισχύουν:
abc=1 και ab+bc+ca=a+b+c.
Να αποδείξετε ότι ένας τουλάχιστον από τους αριθμούς αυτούς είναι ίσος με το 1.
Ετικέτες
Α' Λυκείου,
Γ΄ Γυμνασίου
Ανισότητα με πλευρές τριγώνου και τρεις τυχαίους πραγματικούς
Αν  πλευρές τριγώνου και
πλευρές τριγώνου και  πραγματικοί, να δείξετε ότι :
πραγματικοί, να δείξετε ότι :
 .
.
Πότε ισχύει η ισότητα;
 πλευρές τριγώνου και
πλευρές τριγώνου και  πραγματικοί, να δείξετε ότι :
πραγματικοί, να δείξετε ότι : .
.Πότε ισχύει η ισότητα;
Παναγιώτης Λώλας
Ετικέτες
Ανισότητες,
Μαθηματικοί Διαγωνισμοί
Ελάχιστο παράστασης
Να υπολογιστεί το ελάχιστο της παράστασης
$$x^2-8xy+19y^2-6y+3$$
προσδιορίζοντας ταυτόχρονα και τις τιμές των $x,y$ για τις οποίες το έχουμε.
προσδιορίζοντας ταυτόχρονα και τις τιμές των $x,y$ για τις οποίες το έχουμε.
Ετικέτες
Α' Λυκείου,
Γ΄ Γυμνασίου
Ανισότητα ακεραίων
Αν  είναι θετικοί ακέραιοι να αποδείξετε ότι
είναι θετικοί ακέραιοι να αποδείξετε ότι
 είναι θετικοί ακέραιοι να αποδείξετε ότι
είναι θετικοί ακέραιοι να αποδείξετε ότι ![\sqrt[a+b]{a^{2a}b^{2b}}\leq a^2-ab+b^2. \sqrt[a+b]{a^{2a}b^{2b}}\leq a^2-ab+b^2.](https://www.mathematica.gr/forum/ext/geomar/texintegr/latexrender/pictures/37aa84672915779315d615a83f7c5dfd.png)
Θεαίτητος, 1ο τεύχος
Μανόλης Μαραγκάκης
Ετικέτες
Ανισότητες,
Μαθηματικοί Διαγωνισμοί
Προπολεμικό πρόβλημα! (1938-39)
Σε ορθογώνιο τρίγωνο  (με ορθή γωνία
(με ορθή γωνία  ) δίνονται οι τρεις πλευρές
) δίνονται οι τρεις πλευρές  .
.
Να βρεθεί πάνω στην υποτείνουσα σημείο
σημείο  τέτοιο ώστε ο λόγος
τέτοιο ώστε ο λόγος 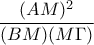 να είναι ίσος με
να είναι ίσος με  . (Διερεύνηση)
. (Διερεύνηση)
 (με ορθή γωνία
(με ορθή γωνία  ) δίνονται οι τρεις πλευρές
) δίνονται οι τρεις πλευρές  .
.Να βρεθεί πάνω στην υποτείνουσα
 σημείο
σημείο  τέτοιο ώστε ο λόγος
τέτοιο ώστε ο λόγος 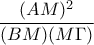 να είναι ίσος με
να είναι ίσος με  . (Διερεύνηση)
. (Διερεύνηση)
Πανελλήνιος Μαθηματικός Διαγωνισμός, 1938-39
(Πρακτικού Λυκείου)
Ετικέτες
Β΄ Λυκείου,
Μαθηματικοί Διαγωνισμοί
Σύνολα ακεραίων
Προσδιορίστε όλα τα σύνολα  θετικών ακεραίων τέτοια ώστε για οποιαδήποτε δύο,
θετικών ακεραίων τέτοια ώστε για οποιαδήποτε δύο,
 θετικών ακεραίων τέτοια ώστε για οποιαδήποτε δύο,
θετικών ακεραίων τέτοια ώστε για οποιαδήποτε δύο,
όχι απαραίτητα διαφορετικά, στοιχεία  του
του  ο αριθμός
ο αριθμός  να ανήκει στο
να ανήκει στο 
 του
του  ο αριθμός
ο αριθμός  να ανήκει στο
να ανήκει στο 
Ετικέτες
Μαθηματικοί Διαγωνισμοί
Τετάρτη 22 Ιουλίου 2020
Το άθροισμά τους είναι ίσο με το ΕΚΠ τους!
α) Να βρείτε τρεις θετικούς ακέραιους αριθμούς με την ιδιότητα το άθροισμά τους να είναι ίσο με το ελάχιστο κοινό πολλαπλάσιό τους.
β) Να βρείτε 100 θετικούς ακέραιους αριθμούς με την ιδιότητα το άθροισμά τους να είναι ίσο με το ελάχιστο κοινό πολλαπλάσιό τους.
Διαγωνισμός Πόλεων, 1995
γ) Να βρείτε 2020 θετικούς ακέραιους αριθμούς με την ιδιότητα το άθροισμά τους να είναι ίσο με το ελάχιστο κοινό πολλαπλάσιό τους.
β) Να βρείτε 100 θετικούς ακέραιους αριθμούς με την ιδιότητα το άθροισμά τους να είναι ίσο με το ελάχιστο κοινό πολλαπλάσιό τους.
Διαγωνισμός Πόλεων, 1995
γ) Να βρείτε 2020 θετικούς ακέραιους αριθμούς με την ιδιότητα το άθροισμά τους να είναι ίσο με το ελάχιστο κοινό πολλαπλάσιό τους.
Ετικέτες
Α΄ Γυμνασίου,
Β΄ Γυμνασίου,
Γ΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Τρίτη 21 Ιουλίου 2020
Γωνία 60 μοιρών με κορυφή το περίκεντρο ισοπλεύρου τριγώνου
Δίνεται ισόπλευρο τρίγωνο  με πλευρά με πλευρά  και περίκεντρο και περίκεντρο  . Επί των πλευρών . Επί των πλευρών  παίρνουμε αντίστοιχα σημεία παίρνουμε αντίστοιχα σημεία  , τέτοια ώστε , τέτοια ώστε 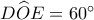 . Δείξτε ότι η περίμετρος του τριγώνου . Δείξτε ότι η περίμετρος του τριγώνου  ισούται με ισούται με  . .
Μιχάλης Νάννος, Σαλαμίνα
|
Ετικέτες
Α' Λυκείου,
Γ΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Κάπου υπάρχει λάθος
Σ' ένα χορό πήραν μέρος 8 αγόρια και 8 κορίτσια. Κάθε αγόρι χόρεψε με μερικά κορίτσια και κάθε κορίτσι με μερικά αγόρια. Μετά το τέλος του χορού κάθε άτομο έγραψε, στη σειρά, τον αριθμό των χορών που χόρεψε. Έτσι πήραμε τους αριθμούς: 3, 3, 3, 3, 3, 3, 4, 6, 6, 6, 6, 6, 6, 6, 6, 6. Να αποδείξετε ότι οι αριθμοί αυτοί δεν είναι οι σωστοί, γιατί κάπου υπάρχει λάθος.
Ευκλείδης, Β' Γυμνασίου, 1995
Ετικέτες
Α' Λυκείου,
Β΄ Γυμνασίου,
Γ΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Ανισότητα με πλευρές τριγώνου (1)
Σε τρίγωνο  αποδείξτε ότι
αποδείξτε ότι
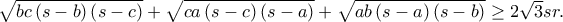
 αποδείξτε ότι
αποδείξτε ότι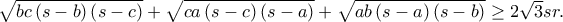
Διευκρίνηση: a, b, c είναι οι πλευρές του τριγώνου
s είναι η ημιπερίμετρος του τριγώνου
r είναι η ακτίνα του εγγεγραμμένου κύκλου του τριγώνου
Ετικέτες
Ανισότητες,
Γ΄ Λυκείου,
Μαθηματικοί Διαγωνισμοί
Ανισότητα με 4 ακεραίους
Αν  είναι τέσσερις διαφορετικοί θετικοί ακέραιοι, να αποδείξετε ότι
είναι τέσσερις διαφορετικοί θετικοί ακέραιοι, να αποδείξετε ότι
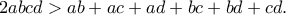
 είναι τέσσερις διαφορετικοί θετικοί ακέραιοι, να αποδείξετε ότι
είναι τέσσερις διαφορετικοί θετικοί ακέραιοι, να αποδείξετε ότι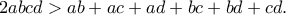
Ετικέτες
Α' Λυκείου,
Β΄ Λυκείου,
Γ΄ Λυκείου,
Μαθηματικοί Διαγωνισμοί
Δευτέρα 20 Ιουλίου 2020
Κυριακή 19 Ιουλίου 2020
200 αυγά
Έχουμε 200 αυγά τα οποία θέλουμε να τοποθετήσουμε σε καλάθια κατά τέτοιο τρόπο, ώστε κάθε καλάθι να περιέχει διαφορετικό αριθμό αυγών. Ποιος είναι ο μέγιστος αριθμός καλαθιών που μπορούν να χρησιμοποιηθούν σε αυτή τη διαδικασία;
Θαλής, Β' Γυμνασίου, 1995
Ετικέτες
Β΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Στρατηγική σε πολύγωνο με άρτιο πλήθος πλευρών
Δυο μαθητές Α και Β παίζουν το ακόλουθο παιχνίδι:
Τους δίνεται ένα κανονικό πολύγωνο με άρτιο πλήθος πλευρών, μεγαλύτερο από 6 (π.χ.ένα 100-γωνο). Κάθε παίκτης συνδέει δυο από τις κορυφές του πολυγώνου με ένα τμήμα το οποίο, όμως, να μην τέμνει κανένα από άλλα τέτοια τμήματα που οι παίκτες είχαν φέρει προηγουμένως. Θα χάσει ο παίκτης που πρώτος δε θα μπορέσει να φέρει ένα τέτοιο τμήμα. Μπορεί ένας παίκτης να ακολουθήσει μια στρατηγική ώστε να νικήσει σίγουρα;
Τους δίνεται ένα κανονικό πολύγωνο με άρτιο πλήθος πλευρών, μεγαλύτερο από 6 (π.χ.ένα 100-γωνο). Κάθε παίκτης συνδέει δυο από τις κορυφές του πολυγώνου με ένα τμήμα το οποίο, όμως, να μην τέμνει κανένα από άλλα τέτοια τμήματα που οι παίκτες είχαν φέρει προηγουμένως. Θα χάσει ο παίκτης που πρώτος δε θα μπορέσει να φέρει ένα τέτοιο τμήμα. Μπορεί ένας παίκτης να ακολουθήσει μια στρατηγική ώστε να νικήσει σίγουρα;
Θαλής, Α' Λυκείου, 1995
Ετικέτες
Α' Λυκείου,
Μαθηματικοί Διαγωνισμοί
Ο ταμίας έχει περισσότερα νομίσματα των 20 λεπτών από αυτά των 10 λεπτών.
Ένας ταμίας έχει 500 λεπτά σε νομίσματα των 10, 15, 20 λεπτών. Ο συνολικός αριθμός των νομισμάτων είναι 30. Να αποδείξετε ότι ο ταμίας έχει περισσότερα νομίσματα των 20 λεπτών από αυτά των 10 λεπτών.
Διαγωνισμός πόλεων, 1995
Ετικέτες
Β΄ Γυμνασίου,
Μαθηματικοί Διαγωνισμοί
Σάββατο 18 Ιουλίου 2020
Οι τρεις ακρίδες
Τρεις ακρίδες Α, Β, Γ βρίσκονται πάνω σε μία ευθεία. Η Β βρίσκεται στο μέσο μεταξύ των Α και Γ. Κάθε δευτερόλεπτο μία απ' αυτές πηδά πάνω από μία από τις άλλες στο συμμετρικό σημείο ως προς τη δεύτερη. Μετά από μερικά άλματα οι ακρίδες έχουν επιστρέψει στα αρχικά σημεία, όχι κατ' ανάγκη η καθεμία στην αρχική της θέση. Να αποδείξετε ότι η Β επιστρέφει αναγκαστικά στην αρχική της θέση.
Διαγωνισμός Πόλεων, 1995
Ετικέτες
Μαθηματικοί Διαγωνισμοί
Ο πιο μικρός αριθμός που τελειώνει σε 38, διαιρείται με το 38, έχει άθροισμα ψηφίων το 38!
Βρείτε το μικρότερο φυσικό αριθμό ο οποίος τελειώνει σε 38, διαιρείται με το 38 και το άθροισμα των ψηφίων του είναι 38.
Ετικέτες
Μαθηματικοί Διαγωνισμοί
Κυριακή 12 Ιουλίου 2020
Εγγραφή σε:
Σχόλια (Atom)



 η ανίσωση
η ανίσωση