Θέματα της Ιρλανδικής Μαθηματικής Ολυμπιάδας 1988-2021

 Θέματα της Ιρλανδικής Μαθηματικής Ολυμπιάδας 1988-2021

Άθροισμα 6 γωνιών

 Μια ωραία άσκηση που αλίευσα από το εξαιρετικό blog του Σωκράτη Ρωμανίδη eisatopon.

Ο δεκαπλάσιός του είναι τέλειο τετράγωνο και ο εξαπλάσιός του είναι τέλειος κύβος

 Βρείτε τον μικρότερο θετικό ακέραιο $n$ ώστε ο $10n$ να είναι τέλειο τετράγωνο και ο $6n$ να είναι τέλειος κύβος.

Ο μεγαλύτερος γνήσιος διαιρέτης είναι 11πλάσιος του μικρότερου γνήσιου διαιρέτη

Για έναν θετικό ακέραιο $n>1$ γράφουμε όλους τους διαιρέτες του σε αύξουσα σειρά: $1<d_1<...<d_k<n.$ Για πόσους $n$ ισχύει $d_k=11d_1;$

Μέγιστο άθροισμα δύο όρων ακολουθίας

 Για μια ακολουθία $(a_n)$ πραγματικών αριθμών ισχύει ότι $a_{n+1}^2+a_n^2=a_{n+1}+a_n+24$ για κάθε θετικό ακέραιο $n.$ Να βρείτε τη μέγιστη τιμή του αθροίσματος $a_{2022}+a_1.$ 

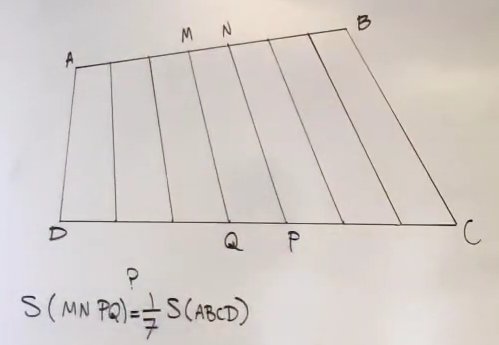
Γκρι και μαύρες περιοχές

 Στο παρακάτω σχήμα κάθε γκρι περιοχή έχει εμβαδόν 72. Βρείτε το συνολικό εμβαδόν των μαύρων περιοχών.

Πράσινο εμβαδόν από την Ελβετία

 Χρησιμοποιώντας έναν διαβήτη φτιάξαμε το παρακάτω σχήμα. Κάθε μικρό τετράγωνο έχει πλευρά 2. Βρείτε το πράσινο εμβαδόν.

Πόσα τετράγωνα μοιράζονται 2 κορυφές με κάποιο τετράγωνο;

 Δίνεται ένα τετράγωνο $ABCD$ σε ένα επίπεδο. Πόσα τετράγωνα του επιπέδου αυτού μοιράζονται με το $ABCD$ ακριβώς δύο κορυφές;

Υπόλοιπο διαίρεσης με το 8

 Τι υπόλοιπο αφήνει η διαίρεση του αριθμού $2^23^35^57^7$ με το $8;$

Περίμετρος πολυγωνικού χωρίου

 Να βρείτε την περίμετρο του παρακάτω σχήματος:

Σύνολο 100 ακεραίων

 Αποδείξτε ότι από ένα σύνολο 100 διαφορετικών ακέραιων αριθμών μπορούμε  πάντα είτε να βρούμε έναν αριθμό που διαιρείται με το 100 είτε μερικούς αριθμούς με άθροισμα που διαιρείται με το 100.

Σύστημα εξισώσεων

 Βρείτε όλες τις τριάδες $(a,b,c)$ πραγματικών αριθμών τέτοιες ώστε $ab+bc+ca=1$ και $a^2b+c=b^2c+a=c^2a+b.$

Πρόβλημα διαιρετότητας από την Ελβετία

Έστω $m,n$ φυσικοί αριθμοί ώστε ο $m+n+1$ να είναι πρώτος και διαιρέτης του αριθμού $2(m^2+n^2)-1.$  Να αποδείξετε ότι $m=n.$

Σύστημα 2 εξισώσεων με 3 αγνώστους

Να λυθεί στο σύνολο των πραγματικών αριθμών το σύστημα

$$(x-1)(y-1)(z-1)=xyz-1$$

$$(x-2)(y-2)(z-2)=xyz-2$$

Πρόβλημα θεωρίας αριθμών από την Ιαπωνία

Βρείτε όλους τους θετικούς ακέραιους αριθμούς $m,n$ για τους οποίους ο $\dfrac{n^2+1}{2m}$ είναι ακέραιος και ο $2^{n-1}+m+4$ είναι τέλειο τετράγωνο. 

Ιαπωνία, 2020

Μέγιστη τιμή παράστασης με δύο μεταβλητές υπό συνθήκη

 Έστω $x,y\in (-2,2)$ με $xy=-1.$ Να βρείτε την ελάχιστη τιμή της παράστασης $$u=\dfrac{4}{4-x^2}+\dfrac{9}{9-y^2}.$$

Εξίσωση με τέσσερις αγνώστους από τη Μολδαβία

 Να λυθεί στους πραγματικούς αριθμούς η εξίσωση

$$x^2+y^2+z^2+t^2=xy+yz+zt+tx-\dfrac{2}{5}.$$

                                        Μαθηματική Ολυμπιάδα Μολδαβίας, 2001

Ανισότητα από τη Μολδαβία

 Αν $x,y\in [1,\dfrac{3}{2}]$ να αποδείξετε ότι 

$$y\sqrt{3-2x}+x\sqrt{3-2y}\leq x^2+y^2.$$ 

Πότε ισχύει η ισότητα;

Σύστημα με κομψή λύση

 Να λύσετε στους πραγματικούς αριθμούς το σύστημα 

$$x^3+9x^2y=10$$

$$y^3+xy^2=2$$

Δύο εξισώσεις με τρεις αγνώστους από την Τουρκία

 Να βρείτε όλες τις τριάδες ακεραίων $x,y,z$ που ικανοποιούν τις εξισώσεις

$$x-yz=11$$

$$xz+y=13$$

Ανισότητα από το Βιετνάμ!

 Αποδείξτε ότι αν $a,b,c,d$ είναι θετικοί αριθμοί τότε

$$\dfrac{1}{\dfrac{1}{a}+\dfrac{1}{b}}+\dfrac{1}{\dfrac{1}{c}+\dfrac{1}{d}}\leq\dfrac{1}{\dfrac{1}{a+c}+\dfrac{1}{b+d}}. $$

Ο αριθμός 712!+1 είναι πρώτος ή σύνθετος;

 Ο αριθμός $712!+1$ είναι πρώτος ή σύνθετος;

Αριθμοί στο (0,1)

Αν $a,b\in (0,1)$ με $\dfrac{a^4+b^4-1}{a^6+b^6-1}=\dfrac{2}{3},$ να αποδείξετε ότι $a^2+b^2=1.$

Πρόβλημα των Romanta Ghita και Ioan Ghita, Ρουμανία

Σύστημα με απόλυτες τιμές

Βρείτε τους αριθμούς $x,y$ αν γνωρίζετε ότι

$$|x-1|+|y-5|=1$$

$$|x-1|-y=-5.$$

Ισοσκελή τρίγωνα μέσα σε ορθογώνιο τρίγωνο

 Υπολογίστε σε μοίρες τη γωνία $x$.

Μέγιστη τιμή συνάρτησης με απόλυτα

 Να βρείτε τη μέγιστη τιμή της συνάρτησης 

$$f(x)=\dfrac{1}{1+|x|}+\dfrac{1}{1+|x-1|}.$$

Ανισότητα με συνθήκη δύο μεταβλητών

Αν  $a,b \in (0,+\infty)$ με $a\cdot b=1,$ να αποδείξετε ότι

$$(a-2)^2+(b-2)^2\geq 2.$$

Άγνωστοι προσθετέοι, γνωστό το άθροισμα!

 Αν $a,b$ είναι πραγματικοί αριθμοί ώστε $a^3-3a^2+5a-17=0$ και $b^3-3b^2+5b+11=0,$ 

να υπολογίσετε το άθροισμα $a+b.$

Αμερικάνικες ακολουθίες!

Οι ακολουθίες $(x_n),(y_n)$ ορίζονται ως εξής:

$x_0=y_0=7$

$x_n=4x_{n-1}+3y_{n-1}$ και

$y_n=2x_{n-1}+3y_{n-1}$ για $n=1,2,... .$

Να υπολογίσετε το όριο $\displaystyle{\lim_{n\to \infty} \dfrac{x_n}{y_n}}.$

Διοφαντική εξίσωση από την Τουρκία

 Να λυθεί στους ακεραίους η εξίσωση 

$$5x^2-6xy+7y^2=383.$$

Ανισότητα από τη Ρουμανία (2)

 Αν $a,b,c>0$ τότε να αποδειχθεί ότι

$$\dfrac{1}{2}\left (\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\right )\geq \dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}$$

Πρόβλημα του Costel Anghel

Ανισότητα από την Ρουμανία

 H Slatina είναι μια πόλη της Ρουμανίας στις όχθες του ποταμού Ολτ. Από εκεί προέρχεται o κατασκευαστής της ακόλουθης ανισότητας:

Αν $a,b,c>0$ με $a+b+c=1$ τότε

$$3(a^2+b^2+c^2)-2(a^3+b^3+c^3)\geq \dfrac{7}{9}.$$

Πρόβλημα του Costel Anghel

Εκθετική εξίσωση (2)

 Να λυθεί στο $\mathbb R$ η εξίσωση

$$3^{4x^3-3x}=\dfrac{2x}{4x^2+2x+1}.$$

Ανισότητα με συνθήκη (2)

Οι θετικοί πραγματικοί αριθμοί $a,b,c$ είναι τέτοιοι ώστε $a+b+c=1.$ Να δείξετε ότι 

$$\displaystyle{\frac{bc+a+1}{a^2+1}+\frac{ca+b+1}{b^2+1}+\frac{ab+c+1}{c^2+1}\leq \frac{39}{10}.}$$

Ανισότητα με συνθήκη (1)

 Οι θετικοί πραγματικοί αριθμοί $a,b,c$ είναι τέτοιοι ώστε $ab+bc+ca=3.$ Να δείξετε ότι 

$$\displaystyle{\frac{1}{4+(a+b)^2}+\frac{1}{4+(b+c)^2}+\frac{1}{4+(c+a)^2}\leq \frac{3}{8}.}$$

Εκθετική Εξίσωση (Ι)

 Να λυθεί η εξίσωση

$$\displaystyle{\rm 5^x\sqrt{\frac{1}{2}+x}+7^x\sqrt{\frac{1}{2}-x}=\sqrt{25^x+49^x}}.$$

Μία εξίσωση, τρεις άγνωστοι

 Να λυθεί η εξίσωση:

$$x\sqrt{1 - y^{2}} + y\sqrt{2 - z^2} + z\sqrt{3 - x^2} = 3.$$

Ακέραιο μέρος δύναμης ρίζας πολυωνυμικής εξίσωσης

 Αν $a$ είναι η μεγαλύτερη ρίζα της εξίσωσης $x^3-3x^2+1=0$ να αποδείξετε ότι οι αριθμοί $[a^{1788}]$ και $[a^{1988}]$ είναι πολλαπλάσια του 17.

Σημείωση: Αν $x$ πραγματικός αριθμός τότε με $[x]$ συμβολίζουμε τον μεγαλύτερο ακέραιο που δεν ξεπερνά τον $x.$

Πρόβλημα με εμβαδά από το Ιράν

 

Στο παραπάνω τετράπλευρο $ABCD$ χωρίζουμε τις πλευρές $AB$ και $CD$ σε 7 ίσα μέρη. Σχηματίζονται έτσι 7 τετράπλευρα. Να αποδείξετε ότι το μεσαίο τετράπλευρο $MNPQ$ έχει εμβαδό ίσο με το ένα έβδομο του εμβαδού του $ABCD.$

Τρία τετράγωνα!

 

Στο παραπάνω σχήμα έχουμε τρία διαδοχικά διαφορετικά τετράγωνα. Να δείξετε ότι το εμβαδόν του τετραπλεύρου $ABCD$ ισούται με το εμβαδόν του μεσαίου τετραγώνου πλευράς $a$.

Προτάθηκε από τον κ. Μιχάλη Νάννο.

Μεταβλητές πλευρές, σταθερό εμβαδόν!

 α) Δείξτε ότι όλα τα τρίγωνα με πλευρές $\sqrt {a^2-a+1},\, \sqrt {a^2+a+1},\, \sqrt {4a^2+3}$ όπου $a$ διατρέχει τους θετικούς πραγματικούς, έχουν ίσα εμβαδά.

β) Μπορείτε να ερμηνεύσετε το αποτέλεσμα αυτό;

Προτάθηκε από τον κ. Μιχάλη Λάμπρου.

Πότε είναι τέλειο τετράγωνο;

 Βρείτε όλους τους φυσικούς αριθμούς $n$ τέτοιους ώστε ο αριθμός $|2^n+5^n-65|$ να είναι τέλειο τετράγωνο.

Πρόβλημα από την Ιρλανδία

 Βρείτε όλους τους $a,b\in \mathbb N$ τέτοιους ώστε $a^2b^2-4(a+b)=n^2$ όπου $n\in \mathbb N.$

Πρόβλημα από τη Σουηδία

 Βρείτε όλους τους φυσικούς αριθμούς $n \geq 8$ τέτοιους ώστε $n^{\frac{1}{n-8}}\in \mathbb N.$

Βρείτε την ακτίνα των τριών μικρών ίσων κύκλων

 

Άθροισμα παραγοντικών, τέλειο τετράγωνο

 Να βρεθούν όλοι οι φυσικοί αριθμοί $n\geq 1$, ώστε ο $1!+2!+\cdots +n!$ να είναι τέλειο τετράγωνο.

Σχόλιο: Yπενθυμίζουμε ότι $n!=1\cdot 2\cdot 3\cdots n$ για κάθε $n\geq 1$.

Να είναι και οι δύο τέλεια τετράγωνα

 Να βρεθούν οι τιμές του θετικού ακεραίου $n$ για τις οποίες οι αριθμοί $\displaystyle{9n+16}$ και $\displaystyle{16n+9}$ είναι τέλεια τετράγωνα.

Αλήθεια ή ψέμα

 Αν $\sqrt x>y$ και $x^3>y$ τότε είναι πάντα αλήθεια ότι $x>y;$

(Aν είναι αλήθεια, να γράψετε την απόδειξη, αν όχι να δώσετε ένα αντιπαράδειγμα.)

Να χωριστούν οι αριθμοί από το 1 ως το 18 σε εννέα ζευγάρια με άθροισμα τέλειο τετράγωνο

Να χωριστούν οι αριθμοί $1, \,2, \,3,\,...\,, \, 17, \,18 $ σε εννέα ζευγάρια έτσι ώστε το άθροισμα των δύο αριθμών σε κάθε ζευγάρι να είναι τέλειο τετράγωνο.

Άθροισμα τριών τέλειων τετραγώνων

 Αν $n\ge 1$ φυσικός, να γραφεί ο $99^{2n+1}$ ως άθροισμα τριών τέλειων τετραγώνων.